В этом уроке мы рассмотрим каждую из этих операций по отдельности.
Содержание урокаСложение десятичных дробей
Как мы знаем, десятичная дробь имеет целую и дробную часть. При сложении десятичных дробей, целые и дробные части складываются по отдельности.
Например, сложим десятичные дроби 3,2 и 5,3. Десятичные дроби удобнее складывать в столбик.
Запишем сначала эти две дроби в столбик, при этом целые части обязательно должны быть под целыми, а дробные под дробными. В школе это требование называют «запятая под запятой» .
Запишем дроби в столбик так, чтобы запятая оказалась под запятой:
Начинаем складывать дробные части: 2 + 3= 5. Записываем пятёрку в дробной части нашего ответа:
Теперь складываем целые части: 3 + 5 = 8. Записываем восьмёрку в целой части нашего ответа:
Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой» :
Получили ответ 8,5. Значит выражения 3,2 + 5,3 равно 8,5
На самом деле, не всё так просто, как кажется на первый взгляд. Здесь тоже имеются свои подводные камни, о которых мы сейчас поговорим.
Разряды в десятичных дробях
У десятичных дробей, как и у обычных чисел, есть свои разряды. Это разряды десятых, разряды сотых, разряды тысячных. При этом разряды начинаются после запятой.
Первая цифра после запятой отвечает за разряд десятых, вторая цифра после запятой за разряд сотых, третья цифра после запятой за разряд тысячных.
Разряды в десятичных дробях хранят в себе некоторую полезную информацию. В частности, они сообщают сколько в десятичной дроби десятых частей, сотых частей и тысячных частей.
Например, рассмотрим десятичную дробь 0,345
Позиция, где находится тройка, называется разрядом десятых
Позиция, где находится четвёрка, называется разрядом сотых
Позиция, где находится пятёрка, называется разрядом тысячных

Посмотрим на данный рисунок. Видим, что в разряде десятых располагается тройка. Это говорит о том, что в десятичной дроби 0,345 содержится три десятых .
Если мы сложим дроби , и то получим изначальную десятичную дробь 0,345

Видно, что сначала мы получили ответ , но перевели его в десятичную дробь и получили 0,345.
При сложении десятичных дробей соблюдаются те же принципы и правила, что и при сложении обычных чисел. Сложение десятичных дробей происходит по разрядам: десятые части складываются с десятыми частями, сотые с сотыми, тысячные с тысячными.
Поэтому при сложении десятичных дробей требуют соблюдать правило «запятая под запятой» . Запятая под запятой обеспечивает тот самый порядок, в котором десятые части складываются с десятыми, сотые с сотыми, тысячные с тысячными.
Пример 1. Найти значение выражения 1,5 + 3,4
В первую очередь складываем дробные части 5 + 4 = 9. Записываем девятку в дробной части нашего ответа:
Теперь складываем целые части 1 + 3 = 4. Записываем четвёрку в целой части нашего ответа:
Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой»:
Получили ответ 4,9. Значит значение выражения 1,5 + 3,4 равно 4,9
Пример 2. Найти значение выражения: 3,51 + 1,22
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»
В первую очередь складываем дробную часть, а именно сотые части 1+2=3. Записываем тройку в сотой части нашего ответа:
Теперь складываем десятые части 5+2=7. Записываем семёрку в десятой части нашего ответа:
Теперь складываем целые части 3+1=4. Записываем четвёрку в целой части нашего ответа:
Отделяем запятой целую часть от дробной, соблюдая правило «запятая под запятой»:
Получили ответ 4,73. Значит значение выражения 3,51 + 1,22 равно 4,73
3,51 + 1,22 = 4,73
Как и в обычных числах, при сложении десятичных дробей может произойти . В этом случае в ответе записывается одна цифра, а остальные переносят на следующий разряд.
Пример 3. Найти значение выражения 2,65 + 3,27
Записываем в столбик данное выражение:
Складываем сотые части 5+7=12. Число 12 не поместится в сотой части нашего ответа. Поэтому в сотой части записываем цифру 2, а единицу переносим на следующий разряд:
Теперь складываем десятые части 6+2=8 плюс единица, которая досталась от предыдущей операции, получим 9. Записываем цифру 9 в десятой части нашего ответа:
Теперь складываем целые части 2+3=5. Записываем цифру 5 в целой части нашего ответа:
Получили ответ 5,92. Значит значение выражения 2,65 + 3,27 равно 5,92
2,65 + 3,27 = 5,92
Пример 4. Найти значение выражения 9,5 + 2,8
Записываем в столбик данное выражение
Складываем дробные части 5 + 8 = 13. Число 13 не поместится в дробной часть нашего ответа, поэтому сначала записываем цифру 3, а единицу переносим на следующий разряд, точнее переносим её к целой части:
Теперь складываем целые части 9+2=11 плюс единица, которая досталась от предыдущей операции, получаем 12. Записываем число 12 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 12,3. Значит значение выражения 9,5 + 2,8 равно 12,3
9,5 + 2,8 = 12,3
При сложении десятичных дробей количество цифр после запятой в обеих дробях должно быть одинаковым. Если цифр не хватает, то эти места в дробной части заполняются нулями.
Пример 5 . Найти значение выражения: 12,725 + 1,7
Прежде чем записывать в столбик данное выражение, сделаем количество цифр после запятой в обеих дробях одинаковым. В десятичной дроби 12,725 после запятой три цифры, а в дроби 1,7 только одна. Значит в дроби 1,7 в конце нужно добавить два нуля. Тогда получим дробь 1,700. Теперь можно записать в столбик данное выражение и начать вычислять:

Складываем тысячные части 5+0=5. Записываем цифру 5 в тысячной части нашего ответа:

Складываем сотые части 2+0=2. Записываем цифру 2 в сотой части нашего ответа:

Складываем десятые части 7+7=14. Число 14 не поместится в десятой части нашего ответа. Поэтому сначала записываем цифру 4, а единицу переносим на следующий разряд:

Теперь складываем целые части 12+1=13 плюс единица, которая досталась от предыдущей операции, получаем 14. Записываем число 14 в целой части нашего ответа:

Отделяем запятой целую часть от дробной:

Получили ответ 14,425. Значит значение выражения 12,725+1,700 равно 14,425
12,725+ 1,700 = 14,425
Вычитание десятичных дробей
При вычитании десятичных дробей нужно соблюдать те же правила, что и при сложении: «запятая под запятой» и «равное количества цифр после запятой».
Пример 1. Найти значение выражения 2,5 − 2,2
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»:
Вычисляем дробную часть 5−2=3. Записываем цифру 3 в десятой части нашего ответа:
Вычисляем целую часть 2−2=0. Записываем ноль в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 0,3. Значит значение выражения 2,5 − 2,2 равно 0,3
2,5 − 2,2 = 0,3
Пример 2. Найти значение выражения 7,353 — 3,1
В этом выражении разное количество цифр после запятой. В дроби 7,353 после запятой три цифры, а в дроби 3,1 только одна. Значит в дроби 3,1 в конце нужно добавить два нуля, чтобы сделать количество цифр в обеих дробях одинаковым. Тогда получим 3,100.
Теперь можно записать в столбик данное выражение и вычислить его:

Получили ответ 4,253. Значит значение выражения 7,353 − 3,1 равно 4,253
7,353 — 3,1 = 4,253
Как и в обычных числах, иногда придётся занимать единицу у соседнего разряда, если вычитание станет невозможным.
Пример 3. Найти значение выражения 3,46 − 2,39
Вычитаем сотые части 6−9. От число 6 не вычесть число 9. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда число 6 обращается в число 16. Теперь можно вычислить сотые части 16−9=7. Записываем семёрку в сотой части нашего ответа:
Теперь вычитаем десятые части. Поскольку мы заняли в разряде десятых одну единицу, то цифра, которая там располагалась, уменьшилась на одну единицу. Другими словами, в разряде десятых теперь не цифра 4, а цифра 3. Вычислим десятые части 3−3=0. Записываем ноль в десятой части нашего ответа:
Теперь вычитаем целые части 3−2=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,07. Значит значение выражения 3,46−2,39 равно 1,07
3,46−2,39=1,07
Пример 4 . Найти значение выражения 3−1,2
В этом примере из целого числа вычитается десятичная дробь. Запишем данное выражение столбиком так, чтобы целая часть десятичной дроби 1,23 оказалась под числом 3
Теперь сделаем количество цифр после запятой одинаковым. Для этого после числа 3 поставим запятую и допишем один ноль:
Теперь вычитаем десятые части: 0−2. От нуля не вычесть число 2. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда, 0 обращается в число 10. Теперь можно вычислить десятые части 10−2=8. Записываем восьмёрку в десятой части нашего ответа:
Теперь вычитаем целые части. Раньше в целой располагалось число 3, но мы заняли у него одну единицу. В результате оно обратилось в число 2. Поэтому из 2 вычитаем 1. 2−1=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,8. Значит значение выражения 3−1,2 равно 1,8
Умножение десятичных дробей
Умножение десятичных дробей это просто и даже увлекательно. Чтобы перемножить десятичные дроби, нужно перемножить их как обычные числа, не обращая внимания на запятые.
Получив ответ, необходимо отделить запятой целую часть от дробной. Чтобы сделать это, надо посчитать количество цифр после запятой в обеих дробях, затем в ответе отсчитать справа столько же цифр и поставить запятую.
Пример 1. Найти значение выражения 2,5 × 1,5
Перемножим эти десятичные дроби как обычные числа, не обращая внимания на запятые. Чтобы не обращать внимания на запятые, можно на время представить, что они вообще отсутствуют:

Получили 375. В этом числе необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в дробях 2,5 и 1,5. В первой дроби после запятой одна цифра, во второй дроби тоже одна. Итого две цифры.
Возвращаемся к числу 375 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:

Получили ответ 3,75. Значит значение выражения 2,5 × 1,5 равно 3,75
2,5 × 1,5 = 3,75
Пример 2. Найти значение выражения 12,85 × 2,7
Перемножим эти десятичные дроби, не обращая внимания на запятые:

Получили 34695. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 12,85 и 2,7. В дроби 12,85 после запятой две цифры, в дроби 2,7 одна цифра — итого три цифры.
Возвращаемся к числу 34695 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую:

Получили ответ 34,695. Значит значение выражения 12,85 × 2,7 равно 34,695
12,85 × 2,7 = 34,695
Умножение десятичной дроби на обычное число
Иногда возникают ситуации, когда требуется умножить десятичную дробь на обычное число.
Чтобы перемножить десятичную дробь и обычное число, нужно перемножить их, не обращая внимания на запятую в десятичной дроби. Получив ответ, необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в десятичной дроби, затем в ответе отсчитать справа столько же цифр и поставить запятую.
Например, умножим 2,54 на 2
Умножаем десятичную дробь 2,54 на обычное число 2, не обращая внимания на запятую:

Получили число 508. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,54. В дроби 2,54 после запятой две цифры.
Возвращаемся к числу 508 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:

Получили ответ 5,08. Значит значение выражения 2,54 × 2 равно 5,08
2,54 × 2 = 5,08
Умножение десятичных дробей на 10, 100, 1000
Умножение десятичных дробей на 10, 100 или 1000 выполняется таким же образом, как и умножение десятичных дробей на обычные числа. Нужно выполнить умножение, не обращая внимания на запятую в десятичной дроби, затем в ответе отделить целую часть от дробной, отсчитав справа столько же цифр, сколько было цифр после запятой в десятичной дроби.
Например, умножим 2,88 на 10
Умножим десятичную дробь 2,88 на 10, не обращая внимания на запятую в десятичной дроби:

Получили 2880. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,88. Видим, что в дроби 2,88 после запятой две цифры.
Возвращаемся к числу 2880 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:

Получили ответ 28,80. Отбросим последний ноль — получим 28,8. Значит значение выражения 2,88×10 равно 28,8
2,88 × 10 = 28,8
Есть и второй способ умножения десятичных дробей на 10, 100, 1000. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается вправо на столько цифр, сколько нулей во множителе.
Например, решим предыдущий пример 2,88×10 этим способом. Не приводя никаких вычислений, сразу же смотрим на множитель 10. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 2,88 передвигаем запятую вправо на одну цифру, получим 28,8.
2,88 × 10 = 28,8
Попробуем умножить 2,88 на 100. Сразу же смотрим на множитель 100. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 2,88 передвигаем запятую вправо на две цифры, получаем 288
2,88 × 100 = 288
Попробуем умножить 2,88 на 1000. Сразу же смотрим на множитель 1000. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 2,88 передвигаем запятую вправо на три цифры. Третьей цифры там нет, поэтому мы дописываем ещё один ноль. В итоге получаем 2880.
2,88 × 1000 = 2880
Умножение десятичных дробей на 0,1 0,01 и 0,001
Умножение десятичных дробей на 0,1, 0,01 и 0,001 происходит таким же образом, как и умножение десятичной дроби на десятичную дробь. Необходимо перемножить дроби, как обычные числа, и в ответе поставить запятую, отсчитав столько цифр справа, сколько цифр после запятой в обеих дробях.
Например, умножим 3,25 на 0,1
Умножаем эти дроби, как обычные числа, не обращая внимания на запятые:

Получили 325. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 3,25 и 0,1. В дроби 3,25 после запятой две цифры, в дроби 0,1 одна цифра. Итого три цифры.
Возвращаемся к числу 325 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую. Отсчитав три цифры мы обнаруживаем, что цифры закончились. В этом случае нужно дописать один ноль и поставить запятую:

Получили ответ 0,325. Значит значение выражения 3,25 × 0,1 равно 0,325
3,25 × 0,1 = 0,325
Есть и второй способ умножения десятичных дробей на 0,1, 0,01 и 0,001. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается влево на столько цифр, сколько нулей во множителе.
Например, решим предыдущий пример 3,25 × 0,1 этим способом. Не приводя никаких вычислений сразу же смотрим на множитель 0,1. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 3,25 передвигаем запятую влево на одну цифру. Передвинув запятую на одну цифру влево мы видим, что перед тройкой больше нет никаких цифр. В этом случае дописываем один ноль и ставим запятую. В результате получаем 0,325
3,25 × 0,1 = 0,325
Попробуем умножить 3,25 на 0,01. Сразу же смотрим на множитель 0,01. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 3,25 передвигаем запятую влево на две цифры, получаем 0,0325
3,25 × 0,01 = 0,0325
Попробуем умножить 3,25 на 0,001. Сразу же смотрим на множитель 0,001. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 3,25 передвигаем запятую влево на три цифры, получаем 0,00325
3,25 × 0,001 = 0,00325
Нельзя путать умножение десятичных дробей на 0,1, 0,001 и 0,001 с умножением на 10, 100, 1000. Типичная ошибка большинства людей.
При умножении на 10, 100, 1000 запятая переносится вправо на столько же цифр сколько нулей во множителе.
А при умножении на 0,1, 0,01 и 0,001 запятая переносится влево на столько же цифр сколько нулей во множителе.
Если на первых порах это сложно запомнить, можно пользоваться первым способом, в котором умножение выполняется как с обычными числами. В ответе нужно будет отделить целую часть от дробной, отсчитав справа столько же цифр, сколько цифр после запятой в обеих дробях.
Деление меньшего числа на большее. Продвинутый уровень.
В одном из предыдущих уроков мы сказали, что при делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе – делитель.
Например, чтобы разделить одно яблоко на двоих, нужно в числитель записать 1 (одно яблоко), а в знаменатель записать 2 (двое друзей). В результате получим дробь . Значит каждому другу достанется по яблока. Другими словами, по половине яблока. Дробь это ответ к задаче «как разделить одно яблоко на двоих»

Оказывается, можно решать эту задачу и дальше, если разделить 1 на 2. Ведь дробная черта в любой дроби означает деление, а значит и в дроби это деление разрешено. Но как? Мы ведь привыкли к тому, что делимое всегда больше делителя. А здесь наоборот, делимое меньше делителя.
Всё станет ясным, если вспомнить, что дробь означает дробление, деление, разделение. А значит и единица может быть раздроблена на сколько угодно частей, а не только на две части.
При разделении меньшего числа на большее получается десятичная дробь, в которой целая часть будет 0 (нулевой). Дробная часть же может быть любой.
Итак, разделим 1 на 2. Решим этот пример уголком:
Единицу на два просто так нацело не разделить. Если задать вопрос «сколько двоек в единице» , то ответом будет 0. Поэтому в частном записываем 0 и ставим запятую:
Теперь как обычно умножаем частное на делитель, чтобы вытащить остаток:
Настал момент, когда единицу можно дробить на две части. Для этого справа от полученной единички дописываем ещё один ноль:
Получили 10. Делим 10 на 2, получаем 5. Записываем пятёрку в дробной части нашего ответа:
Теперь вытаскиваем последний остаток, чтобы завершить вычисление. Умножаем 5 на 2, получаем 10
Получили ответ 0,5. Значит дробь равна 0,5
Половину яблока можно записать и с помощью десятичной дроби 0,5. Если сложить эти две половинки (0,5 и 0,5), мы опять получим изначальное одно целое яблоко:

Этот момент также можно понять, если представить, как 1 см делится на две части. Если 1 сантиметр разделить на 2 части, то получится 0,5 см

Пример 2. Найти значение выражения 4: 5
Сколько пятёрок в четвёрке? Нисколько. Записываем в частном 0 и ставим запятую:
Умножаем 0 на 5, получаем 0. Записываем ноль под четвёркой. Сразу же вычитаем этот ноль из делимого:
Теперь начнём дробить (делить) четвёрку на 5 частей. Для этого справа от 4 дописываем ноль и делим 40 на 5, получаем 8. Записываем восьмёрку в частном.

Завершаем пример, умножив 8 на 5, и получив 40:

Получили ответ 0,8. Значит значение выражения 4: 5 равно 0,8
Пример 3. Найти значение выражения 5: 125
Сколько чисел 125 в пятёрке? Нисколько. Записываем 0 в частном и ставим запятую:

Умножаем 0 на 5, получаем 0. Записываем 0 под пятёркой. Сразу же вычитаем из пятёрки 0

Теперь начнём дробить (делить) пятёрку на 125 частей. Для этого справа от этой пятёрки запишем ноль:

Делим 50 на 125. Сколько чисел 125 в числе 50? Нисколько. Значит в частном опять записываем 0

Умножаем 0 на 125, получаем 0. Записываем этот ноль под 50. Сразу же вычитаем 0 из 50
Теперь делим число 50 на 125 частей. Для этого справа от 50 запишем ещё один ноль:
Делим 500 на 125. Сколько чисел 125 в числе 500. В числе 500 четыре числа 125. Записываем четвёрку в частном:

Завершаем пример, умножив 4 на 125, и получив 500

Получили ответ 0,04. Значит значение выражения 5: 125 равно 0,04
Деление чисел без остатка
Итак, поставим в частном после единицы запятую, тем самым указывая, что деление целых частей закончилось и мы приступаем к дробной части:
Допишем ноль к остатку 4
Теперь делим 40 на 5, получаем 8. Записываем восьмёрку в частном:
40−40=0. Получили 0 в остатке. Значит деление на этом полностью завершено. При делении 9 на 5 получается десятичная дробь 1,8:
9: 5 = 1,8
Пример 2 . Разделить 84 на 5 без остатка
Сначала разделим 84 на 5 как обычно с остатком:

Получили в частном 16 и еще 4 в остатке. Теперь разделим этот остаток на 5. Поставим в частном запятую, а к остатку 4 допишем 0

Теперь делим 40 на 5, получаем 8. Записываем восьмерку в частном после запятой:

и завершаем пример, проверив есть ли еще остаток:

Деление десятичной дроби на обычное число
Десятичная дробь, как мы знаем состоит из целой и дробной части. При делении десятичной дроби на обычное число в первую очередь нужно:
- разделить целую часть десятичной дроби на это число;
- после того, как целая часть будет разделена, нужно в частном сразу же поставить запятую и продолжить вычисление, как в обычном делении.
Например, разделим 4,8 на 2
Запишем этот пример уголком:

Теперь разделим целую часть на 2. Четыре разделить на два будет два. Записываем двойку в частном и сразу же ставим запятую:
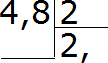
Теперь умножаем частное на делитель и смотрим есть ли остаток от деления:

4−4=0. Остаток равен нулю. Ноль пока не записываем, поскольку решение не завершено. Далее продолжаем вычислять, как в обычном делении. Сносим 8 и делим её на 2

8: 2 = 4. Записываем четвёрку в частном и сразу умножаем её на делитель:

Получили ответ 2,4. Значение выражения 4,8: 2 равно 2,4
Пример 2. Найти значение выражения 8,43: 3

Делим 8 на 3, получаем 2. Сразу же ставим запятую после двойки:

Теперь умножаем частное на делитель 2 × 3 = 6. Записываем шестёрку под восьмёркой и находим остаток:


Делим 24 на 3, получаем 8. Записываем восьмёрку в частном. Сразу же умножаем её на делитель, чтобы найти остаток от деления:

24−24=0. Остаток равен нулю. Ноль пока не записываем. Сносим последнюю тройку из делимого и делим на 3, получим 1. Сразу же умножаем 1 на 3, чтобы завершить этот пример:

Получили ответ 2,81. Значит значение выражения 8,43: 3 равно 2,81
Деление десятичной дроби на десятичную дробь
Чтобы разделить десятичную дробь на десятичную дробь, надо в делимом и в делителе перенести запятую вправо на столько же цифр, сколько их после запятой в делителе, и затем выполнить деление на обычное число.
Например, разделим 5,95 на 1,7
Запишем уголком данное выражение

Теперь в делимом и в делителе перенесём запятую вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит мы должны в делимом и в делителе перенести запятую вправо на одну цифру. Переносим:

После перенесения запятой вправо на одну цифру десятичная дробь 5,95 обратилась в дробь 59,5. А десятичная дробь 1,7 после перенесения запятой вправо на одну цифру обратилась в обычное число 17. А как делить десятичную дробь на обычное число мы уже знаем. Дальнейшее вычисление не составляет особого труда:

Запятая переносится вправо с целью облегчить деление. Это допускается по причине того, что при умножении или делении делимого и делителя на одно и то же число, частное не меняется. Что это значит?
Это одна из интересных особенностей деления. Его называют свойством частного. Рассмотрим выражение 9: 3 = 3. Если в этом выражении делимое и делитель умножить или разделить на одно и то же число, то частное 3 не изменится.
Давайте умножим делимое и делитель на 2, и посмотрим, что из этого получится:
(9 × 2 ) : (3 × 2 ) = 18: 6 = 3
Как видно из примера, частное не поменялось.
Тоже самое происходит, когда мы переносим запятую в делимом и в делителе. В предыдущем примере, где мы делили 5,91 на 1,7 мы перенесли в делимом и делителе запятую на одну цифру вправо. После переноса запятой, дробь 5,91 преобразовалась в дробь 59,1 а дробь 1,7 преобразовалась в обычное число 17.
На самом деле внутри этого процесса происходило умножение на 10. Вот как это выглядело:
5,91 × 10 = 59,1
Поэтому от количества цифр после запятой в делителе зависит то, на что будет умножено делимое и делитель. Другими словами, от количества цифр после запятой в делителе будет зависеть то, на сколько цифр в делимом и в делителе запятая будет перенесена вправо.
Деление десятичной дроби на 10, 100, 1000
Деление десятичной дроби на 10, 100, или 1000 осуществляется таким же образом, как и . Например, разделим 2,1 на 10. Решим этот пример уголком:

Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится влево на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 2,1: 10. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 2,1 нужно перенести запятую влево на одну цифру. Переносим запятую влево на одну цифру и видим, что там больше не осталось цифр. В этом случае перед цифрой дописываем ещё один ноль. В итоге получаем 0,21
Попробуем разделить 2,1 на 100. В числе 100 два нуля. Значит в делимом 2,1 надо перенести запятую влево на две цифры:
2,1: 100 = 0,021
Попробуем разделить 2,1 на 1000. В числе 1000 три нуля. Значит в делимом 2,1 надо перенести запятую влево на три цифры:
2,1: 1000 = 0,0021
Деление десятичной дроби на 0,1, 0,01 и 0,001
Деление десятичной дроби на 0,1, 0,01, и 0,001 осуществляется таким же образом, как и . В делимом и в делителе надо перенести запятую вправо на столько цифр, сколько их после запятой в делителе.
Например, разделим 6,3 на 0,1. В первую очередь перенесём запятые в делимом и в делителе вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит переносим запятые в делимом и в делителе вправо на одну цифру.
После перенесения запятой вправо на одну цифру, десятичная дробь 6,3 превращается в обычное число 63, а десятичная дробь 0,1 после перенесения запятой вправо на одну цифру превращается в единицу. А разделить 63 на 1 очень просто:
Значит значение выражения 6,3: 0,1 равно 63
Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится вправо на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 6,3: 0,1. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 6,3 нужно перенести запятую вправо на одну цифру. Переносим запятую вправо на одну цифру и получаем 63
Попробуем разделить 6,3 на 0,01. В делителе 0,01 два нуля. Значит в делимом 6,3 надо перенести запятую вправо на две цифры. Но в делимом после запятой только одна цифра. В этом случае в конце нужно дописать ещё один ноль. В результате получим 630
Попробуем разделить 6,3 на 0,001. В делителе 0,001 три нуля. Значит в делимом 6,3 надо перенести запятую вправо на три цифры:
6,3: 0,001 = 6300
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
В данной статье мы с Вами разберемся, что такое десятичная дробь, какие у нее есть особенности и свойства. Поехали! 🙂
Десятичная дробь является частным случаем обыкновенных дробей (у которой знаменатель кратен 10).
Определение
Десятичными называют дроби, знаменатели которых представляют собой числа, состоящие из единицы и некоторого количества следующих за нею нулей. То есть это дроби со знаменателем 10, 100, 1000 и т.д. Иначе десятичную дробь можно охарактеризовать как дробь со знаменателем 10 или одной из степеней десятки.
Примеры дробей:
, ,
Десятичная дробь записывается иначе, чем обыкновенная. Операции с этими дробями также отличны от операций с обыкновенными. Правила действий над ними в значительной мере приближены к правилами действий над целыми числами. Этим, в частности, обусловлена их востребованность при решении практических задач.
Представление дроби в десятичной записи
В записи десятичной дроби нет знаменателя, в ней отображено число числителя. В общем виде запись десятичной дроби осуществляется по такой схеме:
где Х – целая часть дроби, Y – ее дробная часть, «,» – десятичная запятая.
Для правильного представления обыкновенной дроби в виде десятичной требуется, чтобы она была правильной, то есть с выделенной целой частью (если это возможно) и числителем, который меньше знаменателя. Тогда в десятичной записи целая часть записывается до десятичной запятой (Х), а числитель обыкновенной дроби – после десятичной запятой (Y).
Если в числителе представлено число с количеством знаков, меньшим, чем количество нулей в знаменателе, то в части Y недостающее количество знаков в десятичной записи заполняется нулями впереди цифр числителя.
Пример:![]()
Если обыкновенная дробь меньше 1, т.е. не имеет целой части, то для Х в десятичном виде записывают 0.
В дробной части (Y), после последнего значимого (отличного от нуля) разряда, может быть вписано произвольное количество нулей. На значение дроби это не влияет. И наоборот: все нули в конце дробной части десятичной дроби можно опустить.
Прочтение десятичных дробей
Часть Х читается в общем случае так: «Х целых».
Часть Y прочитывается в соответствии с числом в знаменателе. Для знаменателя 10 следует читать: «Y десятых», для знаменателя 100: «Y сотых», для знаменателя 1000: «Y тысячных» и так далее… 😉
Более корректным считается другой подход к прочтению, основанный на подсчете количества разрядов дробной части. Для этого нужно понимать, что дробные разряды расположены в зеркальном отражении по отношению к разрядам целой части дроби.
Наименования для правильного прочтения приведены в таблице:

Исходя из этого, прочтение должно опираться на соответствие наименованию разряда последней цифры дробной части.
- 3,5 читается как «три целых пять десятых»
- 0,016 читается как «ноль целых шестнадцать тысячных»
Перевод произвольной обыкновенной дроби в десятичную
Если в знаменателе обыкновенной дроби стоит 10 или какая-нибудь степень десятки, то перевод дроби выполняется как описано выше. В остальных ситуациях необходимы дополнительные преобразования.
Существует 2 способа перевода.
Первый способ перевода
Числитель и знаменатель необходимо домножить на такое целое число, чтобы в знаменателе было получено число 10 или одна из степеней десятки. А далее дробь представляется в десятичной записи.
Этот способ применим для дробей, знаменатель которых раскладывается только на 2 и 5. Так, в предыдущем примере ![]() . Если же в разложении присутствуют другие простые множители (например, ), то придется прибегнуть ко 2-му способу.
. Если же в разложении присутствуют другие простые множители (например, ), то придется прибегнуть ко 2-му способу.
Второй способ перевода
2-й способ заключается в делении числителя на знаменатель в столбик или на калькуляторе. Целая часть, если таковая имеется, в преобразовании не участвует.
Правило деления в столбик, приводящее в результате к десятичной дроби, описано ниже (см. Деление десятичных дробей).
Перевод десятичной дроби в обыкновенную
Для этого следует ее дробную часть (справа от запятой) записать в виде числителя, а результат прочтения дробной части – в виде соответствующего числа в знаменателе. Далее, если это возможно, нужно сократить полученную дробь.
![]()
Конечная и бесконечная десятичная дробь
Конечной называют десятичная дробь, дробная часть которой состоит из конечного количества цифр.
Выше все приведенные примеры содержат именно конечные десятичные дроби. Однако не всякую обыкновенную дробь возможно представить в виде конечной десятичной. Если 1-й способ перевода для данной дроби не применим, а 2-й способ демонстрирует, что деление невозможно завершить, значит, получена может быть только бесконечная десятичная дробь.
В полном виде бесконечную дробь записать невозможно. В неполном же виде такие дроби можно представить:
- как результат сокращения до желательного количества разрядов после запятой;
- в виде периодической дроби.
Периодической называется дробь, у которой после запятой можно выделить повторяющуюся бесконечно последовательность цифр.
Остальные дроби называются непериодическими. Для непериодических дробей допустим только 1-й способ представления (округление).
Пример периодической дроби: 0,8888888… Здесь налицо повторяющаяся цифра 8, которая, очевидно, будет повторяться до бесконечности, поскольку нет оснований предполагать иное. Эта цифра называется периодом дроби .
Периодические дроби бывают чистыми и смешанными. Чистой является десятичная дробь, у которой период начинается непосредственно после запятой. У смешанной дроби до периода после запятой имеется 1 или больше цифр.
54,33333… – периодическая чистая десят.дробь
2,5621212121… – периодическая смешанная дробь
Примеры записи бесконечных десятичных дробей:
Во 2-м примере показано, как правильно оформлять период в записи периодической дроби.
Перевод периодических десятичных дробей в обыкновенные
Для перевода чистой периодической дроби в обыкновенную ее период записывают в числитель, а в знаменатель пишут число, состоящее из девяток в количестве, равном количеству цифр в периоде.
![]()
Смешанная периодическая десятичная дробь переводится следующим образом:
- нужно сформировать число, состоящее из числа, стоящего после запятой до периода, и первого периода;
- из полученного числа вычесть число, стоящее после запятой до периода. Итог составит числитель обыкновенной дроби;
- в знаменателе требуется вписать число, состоящее из кол-ва девяток, равных кол-ву цифр периода, а за ними нулей, кол-во которых равно количеству цифр числа, стоящего после запятой до 1-го периода.
![]()
![]()
Сравнение десятичных дробей
Десятичные дроби сравнивают первоначально по их целым частям. Больше та дробь, у которой больше ее целая часть.
Если целые части одинаковы, то сравнивают цифры соответствующих разрядов дробной части, начиная с первого (с десятых). Здесь действует тот же принцип: больше та из дробей, у которой больше разряд десятых; при равенстве цифр разряда десятых сравнивают разряды сотых и так далее.
Поскольку
![]() , поскольку при равных целых частях и равных десятых в дробной части у 2-й дроби больше цифра сотых.
, поскольку при равных целых частях и равных десятых в дробной части у 2-й дроби больше цифра сотых.
Сложение и вычитание десятичных дробей
Десятичные дроби складывают и вычитают так же, как и целые числа, записав соответствующие цифры друг под другом. Для этого нужно, чтобы друг под другом находились десятичные запятые. Тогда единицы (десятки и т.д.) целой части, а также десятые (сотые и т.д.) дробной окажутся в соответствии. Недостающие разряды дробной части заполняют нулями. Непосредственно процесс сложения и вычитания осуществляется так же, как и для целых чисел.
Умножение десятичных дробей
Для умножения десятичных дробей нужно записать их друг под другом, выровняв по последней цифре и не обращая внимания на местоположение десятичных запятых. Затем нужно перемножить числа так же, как и при умножении целых чисел. После получения результата следует пересчитать количество цифр после запятой в обоих дробях и отделить запятой в результирующем числе суммарное количество дробных разрядов. Если разрядов не хватает, то они заменяются нулями.

Умножение и деление десятичных дробей на 10 n
Эти действия просты и сводятся к переносу десятичной запятой. При умножении запятая переносится вправо (дробь увеличивается) на количество знаков, равных количеству нулей в 10 n , где n – произвольная целая степень. То есть некоторое количество цифр переносится из дробной части в целую. При делении, соответственно, запятая переносится влево (число уменьшается), и некоторая часть цифр переносится из целой части в дробную. Если цифр для переноса оказывается недостаточно, то недостающие разряды заполняются нулями.
Деление десятичной дроби и целого числа на целое число и на десятичную дробь
Деление в столбик десятичной дроби на целое число выполняется аналогично делению двух целых чисел. Дополнительно требуется только учет положения десятичной запятой: при сносе цифры разряда, за которым следует запятая, необходимо поставить запятую после текущей цифры формируемого ответа. Далее нужно продолжать делить до получения нуля. Если знаков в делимом для полного деления недостает, в их качестве следует использовать нули.

Аналогично делятся в столбик 2 целых числа, если снесены все цифры делимого, а полное деление еще не завершено. В этом случае после сноса последней цифры делимого ставится десят.запятая в формирующемся ответе, а в качестве сносимых цифр используют нули. Т.е. делимое здесь, по сути, представляют как десятичную дробь с нулевой дробной частью.

Для деления десят.дроби (или целого числа) на десят.число необходимо домножить делимое и делитель на число 10 n , в котором количество нулей равно количеству цифр после десят.запятой в делителе. Таким способом избавляются от десят.запятой в дроби, на которую требуется делить. Далее процесс деления совпадает с описанным выше.
Графическое представление десятичных дробей
Графически десятичные дроби изображаются посредством координатной прямой. Для этого единичные отрезки делят дополнительно на 10 равных долей подобно тому, как на линейке откладываются одновременно сантиметры и миллиметры. Это обеспечивает точное отображение десятичных дробей и возможность объективного их сравнения.
Чтобы дольные деления на единичных отрезках были одинаковыми, следует тщательно продумывать длину самого единичного отрезка. Она должна быть такой, чтобы можно было обеспечить удобство дополнительного деления.
Уже в начальной школе учащиеся сталкиваются с дробями. И потом они появляются в каждой теме. Забывать действия с этими числами нельзя. Поэтому нужно знать всю информацию про обыкновенные и десятичные дроби. Понятия эти несложные, главное - разбираться во всем по порядку.
Зачем нужны дроби?
Окружающий нас мир состоит из целых предметов. Поэтому в долях необходимости нет. Зато повседневная жизнь постоянно наталкивает людей на работу с частями предметов и вещей.
Например, шоколад состоит из нескольких долек. Рассмотрим ситуацию, когда его плитка образована двенадцатью прямоугольниками. Если ее разделить на двоих, то получится по 6 частей. Она хорошо разделится и на троих. А вот пятерым не удастся дать по целому числу долек шоколада.
Кстати, эти дольки - уже дроби. А дальнейшее их деление приводит к появлению более сложных чисел.
Что такое «дробь»?
Это число, состоящее из частей единицы. Внешне оно выглядит как два числа, разделенные горизонтальной или наклонной чертой. Эта черта носит название дробной. Число, записанное сверху (слева), называется числителем. То, что стоит снизу (справа), является знаменателем.
По сути, дробная черта оказывается знаком деления. То есть числитель можно назвать делимым, а знаменатель — делителем.
Какие существуют дроби?
В математике их имеется всего два вида: обыкновенные и десятичные дроби. С первыми школьники знакомятся в начальных классах, называя их просто «дроби». Вторые узнают в 5 классе. Именно тогда появляются эти названия.
Обыкновенные дроби — все те, что записываются в виде двух чисел, разделенных чертой. Например, 4/7. Десятичная — это число, в котором дробная часть имеет позиционную запись и отделяется от целой при помощи запятой. К примеру, 4,7. Учащимся нужно четко уяснить, что два приведенных примера — это совершенно разные числа.
Каждую простую дробь можно записать в виде десятичной. Это утверждение почти всегда верно и в обратном направлении. Существуют правила, которые позволяют записать обыкновенной дробью десятичную дробь.

Какие подвиды имеют указанные виды дробей?
Начать лучше в хронологическом порядке, так как они изучаются. Первыми идут обыкновенные дроби. Среди них можно выделить 5 подвидов.
Правильная. Ее числитель всегда меньше знаменателя.
Неправильная. У нее числитель больше или равен знаменателю.
Сократимая/несократимая. Она может оказаться как правильной, так и неправильной. Важно другое, есть ли у числителя со знаменателем общие множители. Если имеются, то на них полагается разделить обе части дроби, то есть сократить ее.
Смешанная. К ее привычной правильной (неправильной) дробной части приписывается целое число. Причем оно всегда стоит слева.
Составная. Она образуется из двух разделенных друг на друга дробей. То есть в ней насчитывается сразу три дробные черты.
У десятичных дробей есть всего два подвида:
конечная, то есть та, у которой дробная часть ограничена (имеет конец);
бесконечная — число, у которого цифры после запятой не заканчиваются (их можно писать бесконечно).

Как переводить десятичную дробь в обыкновенную?
Если это конечное число, то применяется ассоциация, основанная на правиле — как слышу, так пишу. То есть нужно правильно прочитать ее и записать, но уже без запятой, а с дробной чертой.
В качестве подсказки о необходимом знаменателе, нужно запомнить, что он всегда единица и несколько нулей. Последних нужно написать столько, сколько цифр в дробной части рассматриваемого числа.
Как перевести десятичные дроби в обыкновенные, если их целая часть отсутствует, то есть равна нулю? Например, 0,9 или 0,05. После применения указанного правила, получается, что нужно написать ноль целых. Но оно не указывается. Остается записать только дробные части. У первого числа знаменатель будет равен 10, у второго — 100. То есть указанные примеры ответами будут иметь числа: 9/10, 5/100. Причем последнее оказывается можно сократить на 5. Поэтому результатом для нее нужно записать 1/20.
Как из десятичной дроби сделать обыкновенную, если ее целая часть отлична от нуля? Например, 5,23 или 13,00108. В обоих примерах читается целая часть и записывается ее значение. В первом случае это — 5, во втором — 13. Потом нужно переходить к дробной части. С ними полагается провести ту же операцию. У первого числа появляется 23/100, у второго — 108/100000. Второе значение снова нужно сократить. В ответе получаются такие смешанные дроби: 5 23/100 и 13 27/25000.

Как перевести бесконечную десятичную дробь в обыкновенную?
Если она является непериодической, то такую операцию провести не удастся. Этот факт связан с тем, что каждая десятичная дробь всегда переводится или в конечную или в периодическую.
Единственное, что допускается делать с такой дробью, — это округлять ее. Но тогда десятичная будет приблизительно равно той бесконечной. Ее уже можно превратить в обыкновенную. Но обратный процесс: перевод в десятичную — никогда не даст начального значения. То есть бесконечные непериодические дроби в обыкновенные не переводятся. Это нужно запомнить.
Как записать бесконечную периодическую дробь в виде обыкновенной?
В этих числах после запятой всегда появляются одна или несколько цифр, которые повторяются. Их называют периодом. Например, 0,3(3). Здесь «3» в периоде. Их относят к классу рациональных, так как могут быть преобразованы в обыкновенные дроби.
Тем, кто встречался с периодическими дробями, известно, что они могут быть чистыми или смешанными. В первом случае период начинается сразу от запятой. Во втором — дробная часть начинается с каких-либо цифр, а потом начинается повтор.
Правило, по которому нужно записать в виде обыкновенной дроби бесконечную десятичную, будет разным для указанных двух видов чисел. Чистые периодические дроби записать обыкновенными достаточно просто. Как с конечными, их нужно преобразовать: в числитель записать период, а знаменателем будет цифра 9, повторяющаяся столько раз, сколько цифр содержит период.
Например, 0,(5). Целой части у числа нет, поэтому сразу нужно приступать к дробной. В числитель записать 5, а в знаменатель одну 9. То есть ответом будет дробь 5/9.
Правило о том, как записать обыкновенной десятичную периодическую дробь, являющуюся смешанной.
Посмотреть на длину периода. Столько 9 будет иметь знаменатель.
Записать знаменатель: сначала девятки, потом нули.
Чтобы определить числитель, нужно записать разность двух чисел. Уменьшаемым будут все цифры после запятой, вместе с периодом. Вычитаемым — оно же без периода.
Например, 0,5(8) - запишите периодическую десятичную дробь в виде обыкновенной. В дробной части до периода стоит одна цифра. Значит ноль будет один. В периоде тоже только одна цифра — 8. То есть девятка одна. То есть в знаменателе нужно написать 90.
Для определения числителя из 58 нужно вычесть 5. Получается 53. Ответом к примеру придется записать 53/90.

Как переводятся обыкновенные дроби в десятичные?
Самым простым вариантом оказывается число, в знаменателе которого стоит число 10, 100 и прочее. Тогда знаменатель просто отбрасывается, а между дробной и целой частями ставится запятая.
Бывают ситуации, когда знаменатель легко превращается в 10, 100 и т. д. Например, числа 5, 20, 25. Их достаточно умножить на 2, 5 и 4 соответственно. Только умножать полагается не только знаменатель, но и числитель на то же число.
Для всех остальных случаев пригодится простое правило: разделить числитель на знаменатель. В этом случае может получиться два варианта ответов: конечная или периодическая десятичная дробь.
Действия с обыкновенными дробями
Сложение и вычитание
С ними учащиеся знакомятся раньше других. Причем сначала у дробей одинаковые знаменатели, а потом разные. Общие правила можно свести к такому плану.
Найти наименьшее общее кратное знаменателей.
Записать дополнительные множители ко всем обыкновенным дробям.
Умножить числители и знаменатели на определенные для них множители.
Сложить (вычесть) числители дробей, а общий знаменатель оставить без изменения.
Если числитель уменьшаемого меньше вычитаемого, то нужно выяснить, перед нами смешанное число или правильная дробь.
В первом случае у целой части нужно занять единицу. К числителю дроби прибавить знаменатель. А потом выполнять вычитание.
Во втором — необходимо применить правило вычитания из меньшего числа большее. То есть из модуля вычитаемого вычесть модуль уменьшаемого, а в ответ поставить знак «-».
Внимательно посмотреть на результат сложения (вычитания). Если получилась неправильная дробь, то полагается выделить целую часть. То есть разделить числитель на знаменатель.
Умножение и деление
Для их выполнения дроби не нужно приводить к общему знаменателю. Это упрощает выполнение действий. Но в них все равно полагается следовать правилам.
При умножении обыкновенных дробей необходимо рассмотреть числа в числителях и знаменателях. Если какой-либо числитель и знаменатель имеют общий множитель, то их можно сократить.
Перемножить числители.
Перемножить знаменатели.
Если получилась сократимая дробь, то ее полагается снова упростить.
При делении нужно сначала заменить деление на умножение, а делитель (вторую дробь) — на обратную дробь (поменять местами числитель и знаменатель).
Потом действовать, как при умножении (начиная с пункта 1).
В заданиях, где умножить (делить) нужно на целое число, последнее полагается записать в виде неправильной дроби. То есть со знаменателем 1. Потом действовать, как было описано выше.

Действия с десятичными дробями
Сложение и вычитание
Конечно, всегда можно превратить десятичную дробь в обыкновенную. И действовать по уже описанному плану. Но иногда удобнее действовать без этого перевода. Тогда правила для их сложения и вычитания будут совершенно одинаковыми.
Уравнять число цифр в дробной части числа, то есть после запятой. Приписать в ней недостающее количество нулей.
Записать дроби так, чтобы запятая оказалась под запятой.
Сложить (вычесть) как натуральные числа.
Снести запятую.
Умножение и деление
Важно, что здесь не нужно дописывать нули. Дроби полагается оставлять в том виде, как они даны в примере. А дальше идти по плану.
Для умножения нужно написать дроби одна под другой, не обращая внимание на запятые.
Умножить, как натуральные числа.
Поставить в ответе запятую, отсчитав от правого конца ответа столько цифр, сколько их стоит в дробных частях обоих множителей.
Для деления нужно сначала преобразовать делитель: сделать его натуральным числом. То есть умножить его на 10, 100 и т. д., в зависимости от того, сколько цифр в дробной части делителя.
На то же число умножить делимое.
Разделить десятичную дробь на натуральное число.
Поставить в ответе запятую в тот момент, когда закончится деление целой части.

Как быть, если в одном примере есть оба вида дробей?
Да в математике часто встречаются примеры, в которых нужно выполнить действия над обыкновенными и десятичными дробями. В таких заданиях возможны два пути решения. Нужно объективно взвесить числа и выбрать оптимальный.
Первый путь: представить обыкновенные десятичными
Он подходит, если при делении или переводе получаются конечные дроби. Если хотя бы одно число дает периодическую часть, то этот прием применять запрещено. Поэтому, даже если не нравится работать с обыкновенными дробями, придется считать их.
Второй путь: записать десятичные дроби обыкновенными
Этот прием оказывается удобным, если в части после запятой стоят 1-2 цифры. Если их больше, может получиться очень большая обыкновенная дробь и десятичные записи позволят сосчитать задание быстрее и проще. Поэтому всегда нужно трезво оценивать задание и выбирать самый простой метод решения.
В швейной мастерской было 5 цветов ленты. Красной ленты было больше, чем синей на 2,4 метра, но меньше, чем зеленой на 3,8 метра. Белой ленты было больше, чем черной на 1,5 метра, но меньше, чем зеленой на 1,9 метра. Сколько метров ленты всего было в мастерской, если белой было 7,3 метра?
- Решение
- 1) 7,3 + 1,9 = 9,2 (м) зеленой ленты было в мастерской;
- 2) 7,3 – 1,5 = 5,8 (м) черной ленты;
- 3) 9,2 – 3,8 = 5,4 (м) красной ленты;
- 4) 5,4 - 2,4 = 3 (м) синей ленты;
- 5) 7,3 + 9,2 + 5,8 + 5,4 + 3 = 30,7 (м).
- Ответ: всего в мастерской было 30,7 метров ленты.
Задача 2
Длина прямоугольного участка составляет 19,4 метра, а ширина на 2,8 метра меньше. Вычислите периметр участка.
- Решение
- 1) 19,4 – 2,8 = 16,6(м) ширина участка;
- 2) 16,6 * 2 + 19,4 * 2 = 33,2 + 38,8 = 72(м).
- Ответ: периметр участка равен 72 метра.
Задача 3
Длина прыжка кенгуру может достигать 13,5 метров в длину. Мировой рекорд для человека составляет 8,95 метров. Насколько дальше прыгает кенгуру?
- Решение
- 1) 13,5 – 8,95 = 4,55 (м).
- 2) Ответ: кенгуру прыгает на 4,55 метра дальше.
Задача 4
Самая низкая температура на планете была зарегистрирована на станции Восток в Антарктиде, летом 21 июля 1983 года и составляла -89,2 ° C, а самая жаркая в городке Эль-Азизия, 13 сентября 1922 года составляла +57,8 ° C. Вычисли разницу между температурами.
- Решение
- 1) 89,2 + 57,8 = 147° C.
- Ответ: разница между температурами составляет 147° C.
Задача 5
Грузоподъемность фургона Газель составляет 1,5 тонн, а карьерного самосвала БелАЗ в 24 раза больше. Вычислите грузоподъемность самосвала БелАЗ.
- Решение
- 1) 1,5 * 24 = 36 (тонн).
- Ответ: грузоподъемность БелАЗа 36 тонн.
Задача 6
Максимальная скорость движения Земли по своей орбите 30,27 км/сек, а скорость Меркурия на 17,73 км больше. С какой скоростью Меркурий движется по своей орбите?
- Решение
- 1) 30,27 + 17,73 = 48 (км/сек).
- Ответ: скорость движение Меркурия по орбите 48 км/сек.
Задача 7
Глубина Марианской впадины составляет 11,023 км, а высота самой высокой горы в мире - Джомолунгмы 8,848 км над уровнем моря. Вычисли разницу между этими двумя точками.
- Решение
- 1) 11,023 + 8,848 = 19,871(км).
- Ответ: 19, 871 км.
Задача 8
Для Коли, как и для любого здорового человека, нормальная температура тела 36,6 ° C, а для его четвероногого друга Шарика на 2,2 ° C больше. Какая температура для Шарика считается нормальной?
- Решение
- 1) 36,6 + 2,2 = 38,8° C.
- Ответ: для Шарика нормальная температура тела 38,8° C.
Задача 9
Маляр за 1 день покрасил 18,6 м² забора, а его помощник, на 4,4 м² меньше. Сколько всего м2 забора покрасит маляр и его помощник за рабочую неделю, если она равна пяти дням?
- Решение
- 1) 18,6 – 4,4 = 14,2 (м²) покрасит за 1 день помощник маляра;
- 2) 14,2 + 18,6 = 32,8 (м²) покрасят за 1 день вместе;
- 3) 32,8 *5 = 164 (м²).
- Ответ: за рабочую неделю маляр и его помощник вместе покрасят 164 м² забора.
Задача 10
От двух пристаней навстречу друг другу одновременно отошли два катера. Скорость одного катера 42,2 км/ч второго на 6 км/ч больше. Какое расстояние будет между катерами через 2,5 часа, если расстояние между пристанями 140,5 км?
- Решение
- 1) 42,2 + 6 = 48,2 (км/ч) скорость второго катера;
- 2) 42,2 * 2,5 = 105,5 (км) преодолеет первый катер за 2,5 часа;
- 3) 48,2 * 2,5 = 120,5 (км) преодолеет второй катер за 2,5 часа;
- 4) 140,5 – 105,5 = 35 (км) расстояние от первого катера до противоположной пристани;
- 5) 140,5 – 120, 5 = 20 (км) расстояние от второго катера до противоположной пристани;
- 6) 35 + 20 = 55 (км);
- 7) 140 – 55 = 85 (км).
- Ответ: между катерами будет 85 км.
Задача 11
Каждый день велосипедист преодолевает 30,2 км. Мотоциклист, если бы затрачивал столько же времени, преодолевал бы расстояние в 2,5 раза большее, чем велосипедист. Какое расстояние может преодолеть мотоциклист за 4 дня?
- Решение
- 1) 30,2 * 2,5 = 75,5 (км) за 1 день преодолеет мотоциклист;
- 2) 75,5 * 4 = 302 (км).
- Ответ: мотоциклист может преодолеть за 4 дня 302 км.
Задача 12
В магазине за 1 день было продано 18, 3 кг печенья, а конфет на 2,4 кг меньше. Сколько конфет и печенья вместе было продано в магазине за этот день?
- Решение
- 1) 18,3 – 2, 4 = 15,9 (кг) конфет было продано в магазине;
- 2) 15,9 + 18,3 = 34,2 (кг).
- Ответ: конфет и печенья всего было продано 34,2 кг.
Пример:


Запятая в десятичной дроби отделяет:
1) целую часть от дробной;
2) столько знаков, сколько нулей в знаменателе обыкновенной дроби.

Как перевести десятичную дробь в обыкновенную?
Например, \(0,35\) читается как «ноль целых, тридцать пять сотых». Так и пишем: \(0 \frac{35}{100}\). Целая часть равна нулю, то есть ее можно просто не писать, а дробную часть – сократить на \(5\).
Получим: \(0,35=0\frac{35}{100}=\frac{35}{100}=\frac{7}{20}\).
Еще примеры: \(2,14=2\frac{14}{100}=\frac{214}{100}=\frac{107}{50}\);
\(7,026=7\frac{26}{1000}=\frac{7026}{1000}\).
Этот переход можно делать и быстрее:
Запишите в числитель все число без запятой, а в знаменатель – единицу и столько нулей, столько цифр было отделено запятой.
Звучит сложно, поэтому смотрите картинку:

Как обыкновенную дробь перевести в десятичную?
Для этого надо домножить числитель и знаменатель дроби на такое число, чтобы в знаменателе получилось \(10\), \(100\), \(1000\) и т.д., а потом записать результат в десятичном виде.
Примеры: \(\frac{3}{5}\) \(=\)\(\frac{3\cdot 2}{5\cdot 2}\) \(=\)\(\frac{6}{10}\) \(=0,6\); \(\frac{63}{25}\) \(=\frac{63 \cdot 4}{25\cdot 4}\) \(=\)\(\frac{252}{100}\) \(=2,52\); \(\frac{7}{200}\) \(=\)\(\frac{7 \cdot 5}{200\cdot 5}\) \(=\)\(\frac{35}{1000}\) \(=0,035\).
Этот способ хорошо работает, когда в знаменателе дроби: \(2\), \(5\), \(20\), \(25\)… и т.д., то есть когда сразу понятно, на что надо домножать. Однако в остальных случаях:
Для превращения обыкновенной дроби в десятичную нужно поделить числитель дроби на ее знаменатель.
Например , дробь \(\frac{7}{8}\) проще преобразовать делением \(7\) на \(8\), чем догадываться, что \(8\) можно домножить на \(125\) и получить \(1000\).
Далеко не все обыкновенные дроби без проблем превращаются в десятичные. Точнее, превращаются-то все, но вот записать результат такого превращения бывает весьма трудно. Например, дробь \(\frac{9}{17}\) в десятичном виде будет выглядеть как \(0,52941…\) - и так далее, бесконечный ряд неповторяющихся цифр. Такие дроби обычно оставляют в виде обыкновенных.
Однако некоторые дроби, дающие бесконечный ряд цифр в десятичном виде записаны быть могут. Так происходит в случае, если цифры в этом ряду повторяются. Например, дробь \(\frac{2}{3}\) в десятичном виде выглядит так \(0,66666…\) - бесконечный ряд шестерок. Ее записывают вот так: \(0,(6)\). Содержимое скобки – это как раз и есть бесконечно повторяющаяся часть (так называемый период дроби).
Еще примеры: \(\frac{100}{27}\)
\(=\)\(3,7037037037…=3,(703)\).
\(\frac{579}{110}\)
\(=5,2636363636…=5,2(63)\).
Виды десятичных дробей:

Сложение и вычитание десятичных дробей
Сложение (вычитание) десятичных дробей выполняется так же, как сложение (вычитание) : главное, чтобы запятая во втором числе стояла под запятой в первом.




Умножение десятичных дробей
Чтобы перемножить две десятичные дроби, нужно перемножить их как обычные числа, не обращая внимания на запятые. Потом сложить количество знаков после запятой в первом числе и во втором, а затем отделить полученное количество знаков в итоговом числе, считая справа налево.
Лучше \(1\) раз посмотреть на картинку, чем \(10\) раз прочитать, поэтому наслаждайтесь:

Деление десятичных дробей
Чтобы разделить десятичную дробь на десятичную дробь, надо перенести запятую во втором числе (делителе) до тех пор, пока оно не станет целым. Потом на столько же перенести запятую в первом числе (делимом). Затем нужно разделить получившиеся числа как обычно. При этом в ответе нужно будет не забыть поставить запятую сразу же, как мы «перейдем за запятую» в делимом.
Снова картинка объяснит принцип лучше любого текста.


На практике бывает легче представлять деление как обыкновенную дробь, потом домножением числителя и знаменателя убирать запятые (или просто сразу передвигать запятые, как делали выше), а затем сокращать получившиеся числа.
\(13,12:1,6=\)\(\frac{13,12}{1,6}\) \(=\)\(\frac{13,12·100}{1,6·100}\) \(=\)\(\frac{1312}{160}\) \(=\)\(\frac{328}{40}\) \(=\)\(\frac{82}{10}\) \(=8,2\).
Пример . Вычислите \(0,0625:(\)\(\frac{1}{8}\) \(+\)\(\frac{5}{16}\) \()\cdot 2,8\).
Решение :
|
\(0,0625:(\)\(\frac{1}{8}\)
\(+\)\(\frac{5}{16}\)
\()\cdot 2,8=\) |